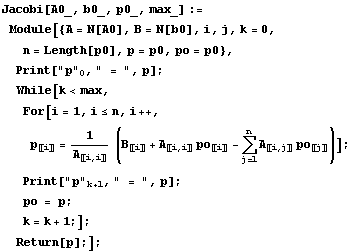
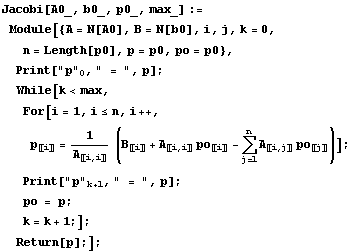
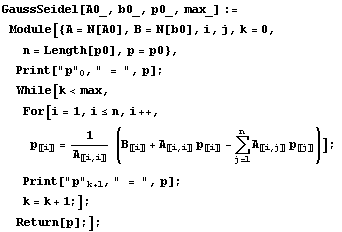
Definujme maticu, pravú stranu, a počiatočný odhad a riešme definovanými iteračnými metódami

Overenie:
![Print["A x = ", MatrixForm[A . x], " ≈ ", MatrixForm[b], " = b"] ;](HTMLFiles/03.png)
Overenie:
![Print["A x = ", MatrixForm[A . x], " ≈ ", MatrixForm[b], " = b"] ;](HTMLFiles/04.png)
Existujú také prípady, že Jacobiho metóda diverduje a Gauss-Seidelova metóda konverguje

![x = GaussSeidel[A, b, p, 5] ;](HTMLFiles/06.png)
Ale aj naopak: Jacobiho metóda konverguje a Gauss-Seidelova metóda diverguje


Prečo je to tak? O tom, či metóda bude konvergovať rozhoduje absolútna hodnota vlastných čisel iteračnej matice (diverguje ak |λ| > 1):
